Every time the Powerball Jackpot gets to be a few hundred million dollars, you may start thinking that buying a ticket sounds like a good idea. But have you ever really considered if it’s really worth it? By using a little bit of math and probabilities, you would actually see that you are pretty much guaranteed to lose money on every ticket you buy.
May the Odds NEVER be in Your Favor
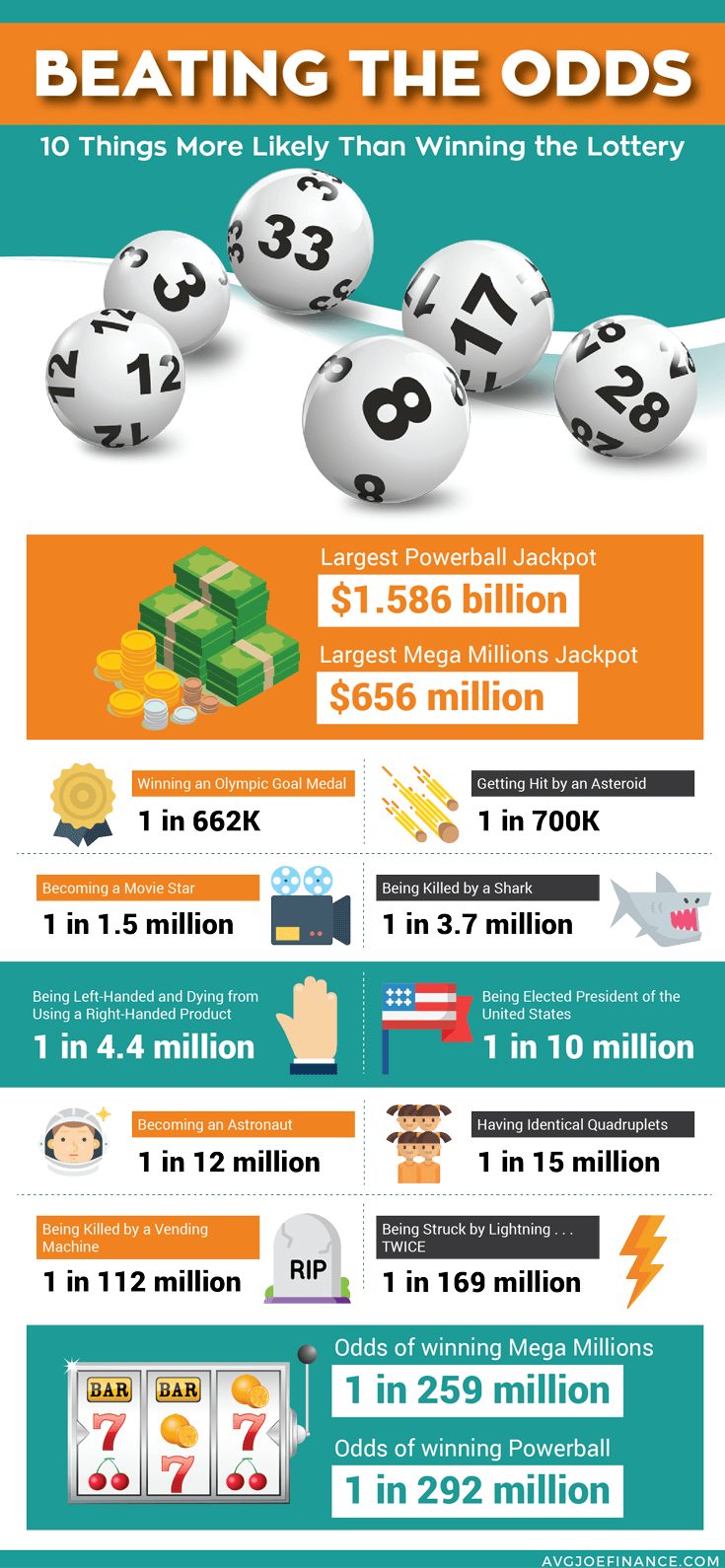
Actually winning the jackpot is pretty much impossible. In fact, the odds of winning the Powerball are around 1 in 292 million. Yet someone has to be that one, right? This logic is what causes so many people to assume that when the jackpot gets big enough, it’s worth the bet. Others may realize they won’t win the jackpot, but figure that since the chance of winning the smaller prizes is better, buying a ticket is still worth it. However, based on the idea of expected value, the jackpot has to be pretty high before you could expect the ticket to be worth more than you paid for it.
Never miss another update. Subscribe today!
What’s Expected Value?
Stay with me here for a minute. Expected value is the mathematical idea of using probabilities to determine the value of a certain outcome. In this case, it is the value of one Powerball ticket. It’s actually pretty easy to determine. You just take the probability of winning each prize and multiply it by the amount of the prize. Then you add up the expected values for all of the prized and subtract the price of a ticket (in this case $2). You need to subtract the price of the ticket because no matter what, you need to pay $2 for the chance to win any prize. See that wasn’t too bad.
| Powerball Odds (1 in X) | Prize Amount | Expected Value |
| 292,201,338.00 | 40,000,000.00 | 0.14 |
| 11,688,053.52 | 1,000,000.00 | 0.09 |
| 913,129.18 | 50,000.00 | 0.05 |
| 36,525.17 | 100.00 | 0.01 |
| 14,494.11 | 100.00 | 0.01 |
| 579.76 | 7.00 | 0.01 |
| 701.33 | 7.00 | 0.01 |
| 91.98 | 4.00 | 0.04 |
| 38.32 | 4.00 | 0.10 |
| Total Expected Value | 0.46 | |
| Ticket Cost | (2.00) | |
| Expected Loss | (1.54) |
As you can see from the chart, at the initial Powerball jackpot value of $40 million, the expected value of a ticket is actually a $1.54 loss. So over the long term, if you only bought Powerball tickets when the jackpot was $40 million, you would expect to lose $1.54 for each ticket you purchased.
When a Ticket is Worth Nothing
As the jackpot grows, the expected value improves, but not by much. At $200 million, the expected value is still a $1 loss per ticket. It’s not until the jackpot reaches $491 million, that the expected value turns positive, but even then it’s less than $.01. And remember if you happen to be the sole winner of a $491 million Powerball jackpot, the only way to get that amount is to take an annuity instead of a lump sum payment. Plus, you will owe a serious amount of taxes which will also lower the amount you can expect to receive. Factoring both of these issues in would drastically increase the jackpot needed for a positive expected value. Higher jackpots typically have multiple winners since more people play, again lowering your actual pay out.
Save Yourself $2
So next time you think it might be a good idea to buy a ticket, save yourself the $2 and put it toward something more useful. Something like your financial future.






My husband and I always sigh when someone wins big..why not us??? Well that’s because we don’t play for these reasons! I used to work at a service desk at a grocery store and saw people wasting so much money, but excited when they won that $1-$5. It was crazy
Low probabilities, high taxes, have to take an annuity — I will still take my chances?!
okay, you’ve convinced me that I will never will the lottery and should keep my 2 bucks in my pocket. But, I have to admit it’s a little fun once in a blue moon to drop a dollar or two and spend the next 24 hours playing the “what would I do with the 3 million dollars if I won” game.
I’m with you that it’s fun to dream about winning, but once I really saw the odds I just dream without buying a ticket. I figure it’s pretty much the same thing.